在数据结构中，我认为红黑树可以说算得上是比较难理解的一种数据结构了，前几天学了红黑树，为了防止随着时间的推移慢慢淡忘，这里记录一下红黑树的实现方法：）））

正文

红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

就二叉树而言，我认为是非常好理解的，但红黑树是基于平衡的二叉树。可能你们不太明白有什么区别，这里我举一个例子，你就能知道二叉树其实也不是万能的！

假设我们往二叉树中插入9,8,7,6,5,4,3,2,1,首先插入9，再一次插入数字，你会发现什么（这图我还做了好久…）

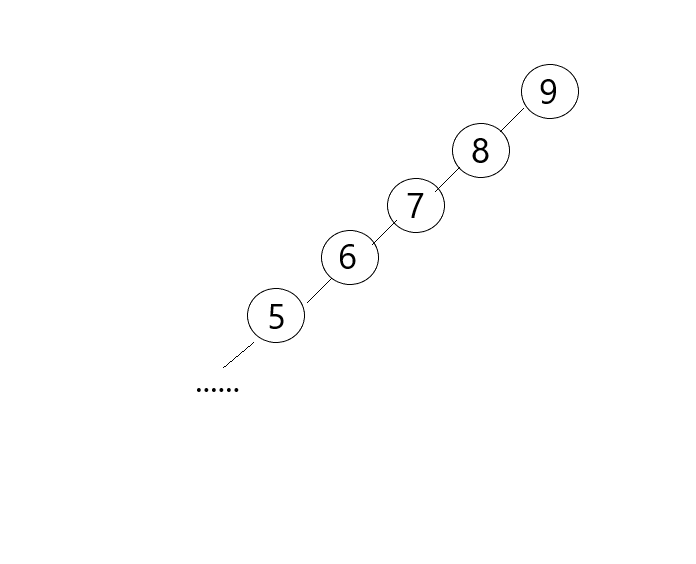
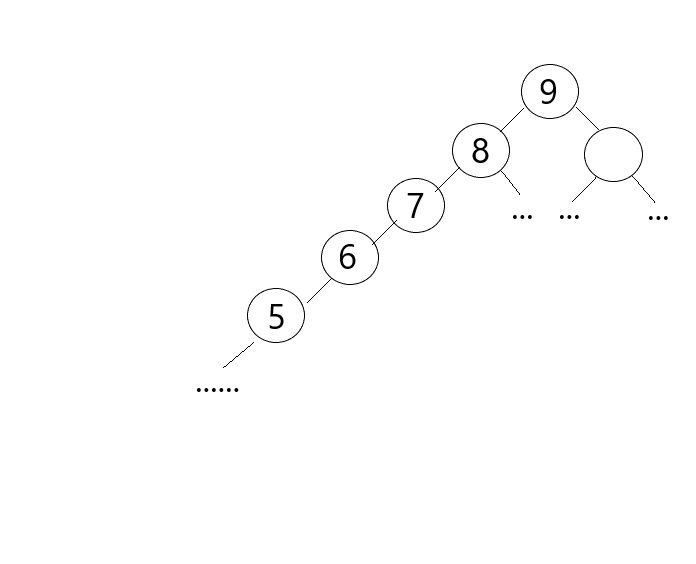
是不是会发现所有的数据都是父节点的左子节点，想一想，如果这在查询的时候，效率是不是很低，原因就是这个树并不平衡。
这时候我们就要考虑如何使这个树平衡，让生成的树像完全二叉树那样。

2-,3-结点

在真正接触红黑树之前，我要先介绍一下2-，3-结点。

· 2-结点：

    含有一个键(及其对用的值)和两条链，左链接的键值都小于该节点，右链接的键值都大于该结点。

· 3-结点：

    含有两个键(及其对应的值)和三条链，左链接指向树中的键都小于该结点，中链接指向树中介于该结点的两键之间，右链接指向树中的键都大于该结点。

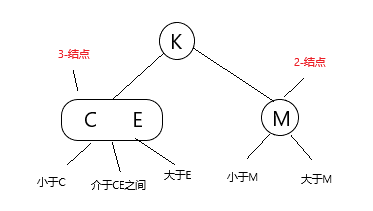
看到这幅图有没有感觉，卧槽还可以这样，的感觉。

而在红黑树中就可以通过链接的颜色来实现这种结构

红黑树

红黑树中的链接分为两种类型：

红链接：将两个2-结点连接起来，构成一个3-结点（上图中的3-结点）；
黑链接：是普通的节点

简单来说，要实现上图的那种结构，我们只需要如图所示即可

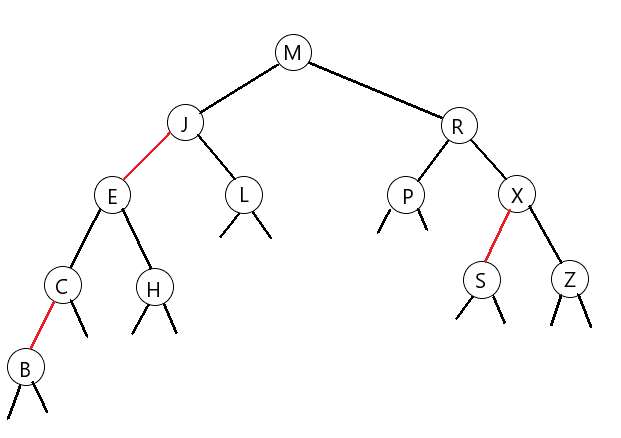
E-J,就相当于C-E。

红黑树定义

1、红链接均为左链接
2、没有任何一个结点同时和两条红链接相连；
3、该树是完美黑色平衡，即任意空链接到根结点的路径上的黑链接树都相等

红黑树中的属性

先介绍红黑树中要用到的几个属性
key–键值
value–存储的值
letf–指向该结点的左节点
right–指向该结点的右结点
color–判断链接的颜色（判断的是父节点指向该结点的链接的颜色）

因为每个结点都有指向自己的链接（从它的父节点指向它），因此我们可以用color来表示链接的颜色，
如果链接为红，bool型为true，为黑，bool型为false；

#define null NULL
#define true 1
#define false 0
#define Key int
#define Value int
#define LEN sizeof(struct Node)
#define bool int

//结点
struct Node
{
    /* data */
    //储存键
    Key key;
    //储存值
    Value value;
    //记录左子节点
    struct Node *left;
    //记录右子节点
    struct Node *right;
    //由其父节点指向它的链接的颜色
    bool color;
};

typedef struct Node* Tree;

//记录根节点
Tree root;
//记录树中元素的个数
int N=0;
//红色链接
#define red true
//黑色链接
#define black false

红黑树的平衡实现

在对红黑树进行增删改查之后，可能会打乱红黑树的平衡，所以我们要做出一些操作来保持红黑树的平衡。

1、左旋；
2、右旋；
3、颜色反转

——————持续更新中——————