这个学期有一门算法课，所以现在打算开始比较系统地学习一些经典的算法以及思想。

分而治之思想

“分而治之”( Divide and conquer)方法(又称“分治术”) ，是有效算法设计中普遍采用的一种技术。

所谓“分而治之” 就是把一个复杂的算法问题按一定的“分解”方法分为等价的规模较小的若干部分，然后逐个解决，分别找出各部分的解，把各部分的解组成整个问题的解。

对于一些问题，如果我们使用枚举法，并不能满足于时间复杂度的需求，此时，分而治之法就是一个不错的选择。
例如对于很经典的排序问题，如果我们使用爆破枚举的方法去解决，时间复杂度是n²,而如果用归并排序(分治术)去设计的话，时间复杂度就是nlogn了。

分而治之可以用我们平常说的大事化小来理解。

而在分治术中，很经典的问题之一就是最大子数组和问题了。

最大子数组和问题

输入：
            给定一个数组X[1..n],对于任意一对数组下标为l,r(l<=r)的非空子数组，其和记为:
                                                    S(l,r)=sum(X[i]) (l<=i<=r)

输出：
             求出S(l,r)的最大值，记为Smax

方法一 暴力枚举

意思就是在下标l-r的数组中，找出和最大的子数组。

这题难度对于没有进行过算法练习的人来讲，很容易想到的就是枚举法：

int Enum(int arr[], int n){
	int max = -128;		// 这里是将max设置为无限小
	int temp;
	int l,r,i;
	for(l=0; l<n; l++){	// 一层循环
		for(r=l; r<n; r++){	// 二层循环
			temp = 0;
			for(i=l; i<=r; i++){	// 三层循环
				temp += arr[i];
			}
			if(max < temp){
				max = temp;
			}
		}
	}
	return max;	// 返回找到的最大值
}

暴力枚举法的总体思路就是，将每一种可能都进行遍历，选出最大值。
对于第一层循环，是先将数组l-r下标的数组全部进行遍历
对于第二层循环，是基于第一层循环下的基础上，对于含有arr[l]的子数组进行遍历
对于第三层循环，是将每一种可能进行全部累加

爆破枚举的时间复杂度非常高，达到了O(N³)

方法二 优化枚举

仔细分析一下我们上面设计的代码，可以发现，对于第三层的循环是很多余的，存在重复计算，我们完全可以去除这一层循环。
思路是，对于第二层循环，我们将temp保留，这样就可以减少一次循环

int Enum_Optimize(int arr[], int n){
	int max = -128;
	int temp;
	int l,r;
	for(l=0; l<n; l++){	// 一层循环
		temp = 0;
		for(r=l; r<n; r++){	// 二层循环
			temp += arr[r];
			if(max < temp){
				max = temp;
			}
		}
	}
	return max;
}

和暴力枚举的区别并不大，但优化之后的枚举，时间复杂度为O(N²)，相比暴力枚举大大减少

方法三 分而治之

运用分治法解决这题的思路就是，分解原问题 --> 解决子问题 --> 合并问题解

先将数组的从中间分开，确定左子数组中的最大值和右子数组中的最大值，接着取存在arr[mid]和arr[mid+1]的子数组的最大值，最后合并左子数组和右子数组取三者的最大值，即为这段子数组的最大值。而其中，左子数组和右子数组则继续采用分治法来计算。

结合主要思想，我们需要的第一步就是通过递归的方法，利用树的思想，大化小，如下图所示:

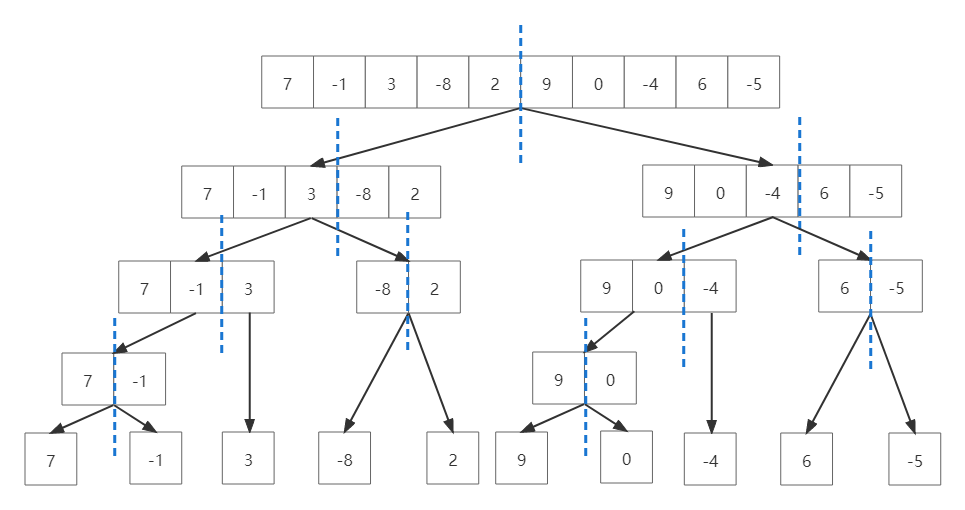
而第二步就是当我们合并不可分割的叶子节点时，如何确定合并后的最大值。
这里需要解决的问题是，当我们合并两个子节点时，可以发现左子节点和右子节点合并后会影响合并后的最大值，并不是取前者或者后者的最大值。
可以发现，合并时取包含arr[mid]和arr[mid+1]的子数组的最大值(通过遍历mid到left，mid+1到right，取出Max[l…mid,mid+1…r])，再取max{left、mid、right}，此时便可以取出合并后的最大值了,思路如下图所示:

此数组的最大子数组和为14

分治法代码如下:

// 解决合并后的数组
int CrossingSubArray(int arr[], int low, int mid, int high){ 
	int Sleft = -128;		// 这里是将最大值设置为无限小
	int Sright = -128;
	int Ssum = 0;
	int i,s3;
	// 取出左子数组的最大值,赋值给Sleft
	for(i=mid; i>=low; i--){
		Ssum += arr[i];
		Sleft = Sleft > Ssum ? Sleft : Ssum;
	}
	Ssum = 0;
	// 取出右子数组的最大值,赋值给Sright
	for(i=mid+1; i<=high; i++){
		Ssum += arr[i];
		Sright = Sright > Ssum ? Sright : Ssum;
	}
	// 返回Sleft+Sright
	s3 = Sleft + Sright;
  return s3;
}

// 分解原问题
int MaxSubArray(int arr[], int low, int high){
	if(low == high){
		return arr[low];
	}
	int mid = (low + high) / 2;
	int s1 = MaxSubArray(arr, low, mid);
	int s2 = MaxSubArray(arr, mid+1, high);
	int s3 = CrossingSubArray(arr, low, mid, high);
	int result = s1 > s2 ? (s1 > s3 ? s1 : s3) : (s2 > s3 ? s2 : s3);
	return result;
}

// 主函数
int main(){
	int arr[] = {7,-1,3,-8,2,9,0,-4,6,-5};
	int num = 10;
	//int max_arr = Enum(arr, num);
	//int max_arr = Enum_Optimize(arr, num);
	int max_arr = MaxSubArray(arr, 0, 9);
	printf("%d\n", max_arr);
	return 0;
}

输出如下:

14

分析时间复杂度的话，可以看出，其主要时间是花费在递归和解决合并子问题，其时间复杂度为nlogn

总结

我们分析了最大子数组问题，可以发现从枚举思想到分治法思想，算法所用到的时间复杂度大大降低，虽不易理解，但也不算太难。(之后我也会介绍关于动态规划的思想怎么去解决这个问题，此时便可以将时间复杂度降低到n，可以期待一下)